题目内容
已知f(x)=
x2-mlnx(m∈R)
(Ⅰ)当m=2时,求函数f(x)在[1,e]上的最大,最小值.
(Ⅱ)若函数f(x)在(
,+∞)上单调递增,求实数m的取值范围.
| 1 |
| 2 |
(Ⅰ)当m=2时,求函数f(x)在[1,e]上的最大,最小值.
(Ⅱ)若函数f(x)在(
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)当m=2时,f′(x)=x-
=
,由此利用导数性质能求出函数f(x)在[1,e]上的最大,最小值.
(Ⅱ)由f′(x)=x-
(x>0),函数f(x)在(
,+∞)上单调递增,由此利用导数性质能求出实数m的取值范围.
| 2 |
| x |
| x2-2 |
| x |
(Ⅱ)由f′(x)=x-
| m |
| x |
| 1 |
| 2 |
解答:
(本小题共12分)
解:(Ⅰ)当m=2时,f′(x)=x-
=
,
令f′(x)=0,得x=
,…(2分)
当x∈[1,
]时,f′(x)<0,
当x∈[
,e]时,f′(x)>0,
故x=
是函数f(x)在[1,e]上唯一的极小值点,…(4分)
故f(x)min=f(
)=1-ln2.…(5分),
又f(1)=
,f(e)=
e2-2=
>
,
故f(x)max=
.…(7分)
(Ⅱ)f′(x)=x-
(x>0),…(8分)
若函数f(x)在(
,+∞)上单调递增,
则f′(x)≥0在(
,+∞)上恒成立,
即m≤x2在(
,+∞)上恒成立,即m≤
.…(11分)
即实数m的取值范围为(-∞,
].…(12分)
解:(Ⅰ)当m=2时,f′(x)=x-
| 2 |
| x |
| x2-2 |
| x |
令f′(x)=0,得x=
| 2 |
当x∈[1,
| 2 |
当x∈[
| 2 |
故x=
| 2 |
故f(x)min=f(
| 2 |
又f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| e2-4 |
| 2 |
| 1 |
| 2 |
故f(x)max=
| e2-4 |
| 2 |
(Ⅱ)f′(x)=x-
| m |
| x |
若函数f(x)在(
| 1 |
| 2 |
则f′(x)≥0在(
| 1 |
| 2 |
即m≤x2在(
| 1 |
| 2 |
| 1 |
| 4 |
即实数m的取值范围为(-∞,
| 1 |
| 4 |
点评:本题考查函数的最大值和最小值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
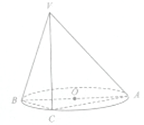 如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=
如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=