题目内容
已知f(x)=3×2x,若g(x)=
,讨论g(x)在(-1,1)上的单调性.
| cxf(x) |
| 2x(x2-1) |
考点:函数单调性的判断与证明
专题:探究型,分类讨论
分析:f(x)=3×2x,若g(x)=
=利用定义法推导出当c>0时g(x)=
,x∈(-1,1)单调递减;当c<0时,g(x)=
,x∈(-1,1)单调递增.
| cxf(x) |
| 2x(x2-1) |
| 3cx |
| x2-1 |
| 3cx |
| x2-1 |
解答:
解:g(x)=
x∈(-1,1),
下面证明单调性:任取-1<x1<x2<1,g(x1)-g(x2)=
-
=
,
由-1<x1<x2<1知
>0,
故当c>0时,g(x1)-g(x2)>0,即g(x1)>g(x2),∴函数g(x)在(-1,1)单调递减;
当c<0时g(x1)-g(x2)<0即g(x1)<g(x2),∴函数g(X)在(-1,1)单调递增.
| cxf(x) |
| 2x(x2-1) |
下面证明单调性:任取-1<x1<x2<1,g(x1)-g(x2)=
| 3cx1 |
| 3(x1)2-1 |
| 3cx2 |
| 3(x2)2-1 |
| 3c(x2-x1)(x1x2+1) |
| ((x1)2-1)((x2)2-1) |
由-1<x1<x2<1知
| 3(x2-x1)(x1x2-1) |
| ((x1)2-1)((x2)2-1) |
故当c>0时,g(x1)-g(x2)>0,即g(x1)>g(x2),∴函数g(x)在(-1,1)单调递减;
当c<0时g(x1)-g(x2)<0即g(x1)<g(x2),∴函数g(X)在(-1,1)单调递增.
点评:本题考查函数的解析式的求法,考查实数的取值范围的求法,考查函数的单调性的判断,解题时要注意函数的性质的合理运用.

练习册系列答案
相关题目
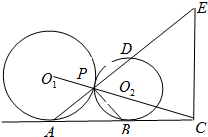 如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.