题目内容
讨论关于x的方程|x2-4x+3|-a=x的根的个数.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:将方程根的问题转化为函数的交点问题,分别讨论①a的范围是[-1,-
]时,②a>-
,或-3<a<-1时,③a=-3时,④a<-3时的情况,从而得出方程的根的个数.
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:利用图象,
y=|x2-4x+3|
y=x+a,直线斜率为1,
画出两个函数的图象,
如图示:
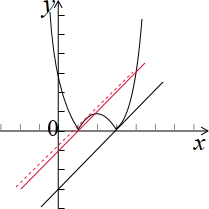
红色实线,过(1,0),则a=-1
红色虚线,过与抛物线相切,
y=-x2+4x-3,和y=x+a相切
-x2+3x-(3+a)=0
∴9+4(3+a)=0
∴a=-
∴①a的范围是[-1,-
]时,图象有3个交点,即方程有3个解;
②a>-
,或-3<a<-1时,图象有2个交点,即方程有2个解;
③a=-3时,图象有1个交点,即方程有1个解;
④a<-3时,图象无交点,即方程无解.
y=|x2-4x+3|
y=x+a,直线斜率为1,
画出两个函数的图象,
如图示:

红色实线,过(1,0),则a=-1
红色虚线,过与抛物线相切,
y=-x2+4x-3,和y=x+a相切
-x2+3x-(3+a)=0
∴9+4(3+a)=0
∴a=-
| 3 |
| 4 |
∴①a的范围是[-1,-
| 3 |
| 4 |
②a>-
| 3 |
| 4 |
③a=-3时,图象有1个交点,即方程有1个解;
④a<-3时,图象无交点,即方程无解.
点评:本题考查了方程的根的问题,考查二次函数的性质,考查转化思想,数形结合思想,分类讨论思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合A={x|-4<x<1},B={x|-3<x<2},则A∩B等于( )
| A、{x|-3<x<1} |
| B、{x|1<x<2} |
| C、{x|x>-3} |
| D、{x|x<1} |
