题目内容
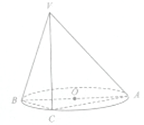 如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=
如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=| 3 |
(Ⅰ)求证:平面VAC⊥平面VBC;
(Ⅱ)求直线VA与平面VBC所成的角.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得VC⊥AC,AC⊥BV.从而AC⊥平面VBC,由此能证明平面VAC⊥平面VBC.
(Ⅱ)由(Ⅰ)知,∠AVC为直线VC与平面VBC所成的角.由此能求出直线V与平面VBC所成的角.
(Ⅱ)由(Ⅰ)知,∠AVC为直线VC与平面VBC所成的角.由此能求出直线V与平面VBC所成的角.
解答:
(Ⅰ)证明:∵VC⊥平面ABC,AC?平面ABC,
∴VC⊥AC.
又C是⊙O上的点,AB是直径,
∴AC⊥BV.
∵VC?平面VAC,BC?平面VAC,VC∩BC=C,
∴AC⊥平面VBC.
又AC?平面VAC,
∴平面VAC⊥平面VBC.…(7分)
(Ⅱ)解:由(Ⅰ)知,∠AVC为直线VC与平面VBC所成的角.
在Rt△ACV中,tan∠AVC=
=
,
∴∠AVC=60°.
∴直线V与平面VBC所成的角为60°.…(13分)
∴VC⊥AC.
又C是⊙O上的点,AB是直径,
∴AC⊥BV.
∵VC?平面VAC,BC?平面VAC,VC∩BC=C,
∴AC⊥平面VBC.
又AC?平面VAC,
∴平面VAC⊥平面VBC.…(7分)
(Ⅱ)解:由(Ⅰ)知,∠AVC为直线VC与平面VBC所成的角.
在Rt△ACV中,tan∠AVC=
| AC |
| VC |
| 3 |
∴∠AVC=60°.
∴直线V与平面VBC所成的角为60°.…(13分)
点评:本题考查平面与平面垂直的证明,考查直线与平面所成的角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目