题目内容
设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(x))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
(3)设函数f(x)的导函数是f′(x),当a=1时求证:对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
(1)若曲线y=f(x)在点(2,f(x))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
(3)设函数f(x)的导函数是f′(x),当a=1时求证:对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由已知得f′(x)=3x2-3a,由此利用导数性质能求出a=4,b=24.
(2)由f′(x)=3(x2-a),a≠0,由此利用导数性质和分类讨论思想能求出函数f(x)的单调区间与极值点.
(3)设x2≥x1>3,要证|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|,只需证x23-3x22-3x2≥x13-3x12-3x1,由此能证明对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
(2)由f′(x)=3(x2-a),a≠0,由此利用导数性质和分类讨论思想能求出函数f(x)的单调区间与极值点.
(3)设x2≥x1>3,要证|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|,只需证x23-3x22-3x2≥x13-3x12-3x1,由此能证明对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
解答:
(1)解:∵f(x)=x3-3ax+b,
∴f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(x))处与直线y=8相切,
∴
,
解得a=4,b=24.
(2)解:∵f′(x)=3(x2-a),a≠0,
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,
此时函数f(x)没有极值点,
当a>0时,由f′(x)=0,得x=±
,
当x∈(-∞,-
)时,f′(x)>0,函数f(x)单调递增,
当x∈(-
,
)时,f′(x)<0,函数f(x)单调递减,
当x∈(
,+∞)时,f′(x)>0,函数f(x)单调递增,
∴x=-
是f(x)的极大值点,x=
是f(x)的极小值点.
(3)证明:不妨设x2≥x1>3,
∵a=1,由(2)知f(x)在(3,+∞)上单调递增,
又f′(x)=3x2-3在(3,+∞)上也单调递增,
∴要证|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|,
只需证x23-3x22-3x2≥x13-3x12-3x1,
设g(x)=x3-3x2-3x,x>3,
g′(x)=3(x2-2x-1),
当x>3时,g′(x)>0,g(x)=x3-3x2-3x在(3,+∞)上单调递增,
∴x23-3x22≥x13-3x12-3x1成立,
∴对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
∴f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(x))处与直线y=8相切,
∴
|
解得a=4,b=24.
(2)解:∵f′(x)=3(x2-a),a≠0,
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,
此时函数f(x)没有极值点,
当a>0时,由f′(x)=0,得x=±
| a |
当x∈(-∞,-
| a |
当x∈(-
| a |
| a |
当x∈(
| a |
∴x=-
| a |
| a |
(3)证明:不妨设x2≥x1>3,
∵a=1,由(2)知f(x)在(3,+∞)上单调递增,
又f′(x)=3x2-3在(3,+∞)上也单调递增,
∴要证|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|,
只需证x23-3x22-3x2≥x13-3x12-3x1,
设g(x)=x3-3x2-3x,x>3,
g′(x)=3(x2-2x-1),
当x>3时,g′(x)>0,g(x)=x3-3x2-3x在(3,+∞)上单调递增,
∴x23-3x22≥x13-3x12-3x1成立,
∴对任意x1,x2∈(3,+∞),|f(x1)-f(x2)|≥|f′(x1)-f′(x2)|成立.
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
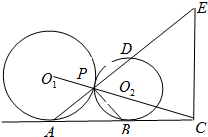 如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2 的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上.