题目内容
已知α,β为钝角,若sin(α+β)=2sin(α-β),则tan(α-β)的最小值是 .
考点:两角和与差的正切函数
专题:三角函数的求值,不等式的解法及应用
分析:由已知可得3tanβ=tanα,根据两角差的正切函数化简可得tan(α-β)=
,结合角的范围,由基本不等式即可求解.
| 2 | ||
|
解答:
解:∵sin(α+β)=2sin(α-β),
⇒sinαcosβ+cosαsinβ=2(sinαcosβ-cosαsinβ)
⇒3cosαsinβ=sinαcosβ
⇒3tanβ=tanα,
∴tan(α-β)=
=
=
,①
∵β为钝角,
∴tanβ<0,
∴
+3tanβ=-(|
|+3|tanβ|)≤-2
,
∴①式≥
=-
.
∴tan(α-β)的最小值是-
.
故答案为:-
.
⇒sinαcosβ+cosαsinβ=2(sinαcosβ-cosαsinβ)
⇒3cosαsinβ=sinαcosβ
⇒3tanβ=tanα,
∴tan(α-β)=
| tanα-tanβ |
| 1+tanαtanβ |
| 2tanβ |
| 1+3tan2β |
| 2 | ||
|
∵β为钝角,
∴tanβ<0,
∴
| 1 |
| tanβ |
| 1 |
| tanβ |
| 3 |
∴①式≥
| 2 | ||
-2
|
| ||
| 3 |
∴tan(α-β)的最小值是-
| ||
| 3 |
故答案为:-
| ||
| 3 |
点评:本题主要考查了两角差的正切公式的应用,考查了基本不等式的应用,属于基本知识的考查.

练习册系列答案
相关题目
变量x、y满足条件
,则(x-2)2+y2的最小值为( )
|
A、
| ||||
B、
| ||||
C、
| ||||
| D、5 |
阅读如图所示的程序框图,若输入的n=10,则该算法的功能是( )
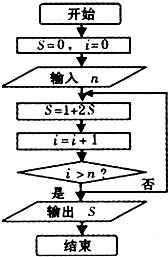

| A、计算数列{2n-1}的前11项和 |
| B、计算数列{2n-1}的前10项和 |
| C、计算数列{2n-1}的前11项和 |
| D、计算数列{2n-1}的前10项和 |