题目内容
求证：函数f（x）=2x3-6x2+7在（0，2）内是减函数．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求出函数的导数，通过f（x）＜0，求出x的范围，从而证得函数f（x）=2x3-6x2在（0，2）内是减函数．
解答：
证明：∵函数f（x）=2x3-6x2+7，
∴f′（x）=6x2-12x，
令f（x）＜0，解得：0＜x＜2，
∴函数f（x）=2x3-6x2在（0，2）内是减函数．
∴f′（x）=6x2-12x，
令f（x）＜0，解得：0＜x＜2，
∴函数f（x）=2x3-6x2在（0，2）内是减函数．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
考前必练系列答案
相关题目
已知二面角α-AB-β的平面角为600，直线OP在平面α内，∠POA=60°，直线m为某几何体的三视图是如图所示，其中左视图为半圆，则该几何体的体积是（ ）
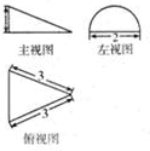
A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
下列函数中，既是奇函数又在区间（0，+∞）上单调递减的是（ ）
| A、y=-x2+2 | ||
B、y=
| ||
| C、y=2-x | ||
| D、y=lnx |
