题目内容
设数列{an}的前n项和为Sn=n2-4n+1,求其通项公式.
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”即可得出.
解答:
解:∵Sn=n2-4n+1,
∴当n=1时,a1=S1=-2;
当n≥2时,an=Sn-Sn-1=n2-4n+1-[(n-1)2-4(n-1)+1]=2n-5.
∴an=
.
∴当n=1时,a1=S1=-2;
当n≥2时,an=Sn-Sn-1=n2-4n+1-[(n-1)2-4(n-1)+1]=2n-5.
∴an=
|
点评:本题考查了递推式的应用,考查了计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若直角坐标平面内A、B两点满足:①点A、B都在函数f(x)的图象上;②点A、B关于原点对称,则点对(A,B)是函数f(x)的一个“姊妹点对”.点对(A,B)与(B,A)可看作是同一个“姊妹点对”,已知函数f(x)=
,则f(x)的“姊妹点对”有 ( )
|
| A、0个 | B、1个 | C、2个 | D、3个 |
要从已编号(1~360)的360件产品中随机抽取30件进行检验,用系统抽样的方法抽出样本,若在抽出的样本中有一个编号为105,则在抽出的样本中最大的编号为( )
| A、355 | B、356 |
| C、357 | D、358 |
某几何体的三视图是如图所示,其中左视图为半圆,则该几何体的体积是( )
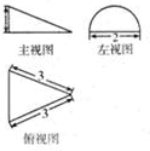

A、
| ||||
B、
| ||||
C、
| ||||
| D、π |