题目内容
已知集合A={（x，y）||x|+2|y|≤4}，集合B={（x，y）|（x-m）2+y2=
}，若B⊆A，则实数m的取值范围是 ．
| 4 |
| 5 |
考点：集合的包含关系判断及应用
专题：集合
分析：根据题意可得集合A的区域是一个关于坐标轴对称的菱形，集合B的区域是一个圆及圆的内部，画出图象即可．
解答：
解：由题意，集合A中元素构成菱形，集合B中元素构成一个圆及圆的内部，
如图
∵B⊆A，
∴圆在菱形内部，
故只需圆心到菱形边坐在的直线的距离大于或等于半径即可，
即：
≥
，
解得m≥-2或m≤-6（舍去），
由对称性可知m≤2，
所以实数m∈[-2，2]．
故答案为：[-2，2]．
解：由题意，集合A中元素构成菱形，集合B中元素构成一个圆及圆的内部，如图
∵B⊆A，
∴圆在菱形内部，
故只需圆心到菱形边坐在的直线的距离大于或等于半径即可，
即：
| |m+4| | ||
|
|
解得m≥-2或m≤-6（舍去），
由对称性可知m≤2，
所以实数m∈[-2，2]．
故答案为：[-2，2]．
点评：本题考查集合间的关系及点到直线的距离公式，做出草图是解决本题的关键，属中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
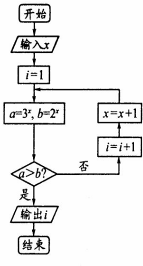
执行如图所示的程序框图，若输入的x的值为-
，则输出的i的值为（ ）
| 3 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
已知不等式
表示的平面区域的面积为2，则
的最小值为（ ）
|
| x+y+2 |
| x+1 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
若非空集合A中的元素具有命题α的性质，集合B中的元素具有命题β的性质，若A?B，则命题α是命题β的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分不必要条件 |
已知二面角α-AB-β的平面角为600，直线OP在平面α内，∠POA=60°，直线m为