题目内容
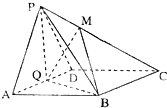 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)点M在线段PC上,PM=
| 1 |
| 3 |
考点:用空间向量求平面间的夹角,平面与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间向量及应用
分析:(1)由题设条件推导出PQ⊥AD,BQ⊥AD,从而得到AD⊥平面PQB,由此能够证明平面PQB⊥平面PAD.
(2)以Q这坐标原点,分别以QA,QB,QP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角M-BQ-C的大小.
(2)以Q这坐标原点,分别以QA,QB,QP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角M-BQ-C的大小.
解答:
解:(1)证明:由题意知:PQ⊥AD,BQ⊥AD,PQ∩BQ=Q,
∴AD⊥平面PQB,
又∵AD?平面PAD,
∴平面PQB⊥平面PAD.
(2)∵PA=PD=AD,Q为AD的中点,
∴PQ⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD,
以Q这坐标原点,分别以QA,QB,QP为x,y,z轴,
建立如图所求的空间直角坐标系,
由题意知:Q(0,0,0),A(1,0,0),
P(0,0,
),B(0,
,0),C(-2,
,0)
∴
=
+
=(-
,
,
),
设
是平面MBQ的一个法向量,则
•
=0,
•
=0,
∴
,∴
=(
,0,1),
又∵
=(0,0,1)平面BQC的一个法向量,
∴cos<
,
>=
,
∴二面角M-BQ-C的大小是60°.
∴AD⊥平面PQB,
又∵AD?平面PAD,
∴平面PQB⊥平面PAD.

(2)∵PA=PD=AD,Q为AD的中点,
∴PQ⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD,
以Q这坐标原点,分别以QA,QB,QP为x,y,z轴,
建立如图所求的空间直角坐标系,
由题意知:Q(0,0,0),A(1,0,0),
P(0,0,
| 3 |
| 3 |
| 3 |
∴
| QM |
| 2 |
| 3 |
| QP |
| 1 |
| 3 |
| QC |
| 2 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
设
| n1 |
| n1 |
| QM |
| n1 |
| QB |
∴
|
| n1 |
| 3 |
又∵
| n2 |
∴cos<
| n1 |
| n2 |
| 1 |
| 2 |
∴二面角M-BQ-C的大小是60°.
点评:本题考查平面与平面垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
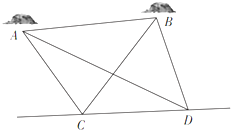 如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面) 如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.
如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°. 用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.
用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.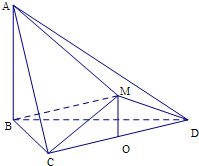 如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2