题目内容
用红，黄，蓝三种颜色涂标有1，2，…，9的小正方形，如图所示，要求相邻的小正方形的颜色不同，标有3，5，7的颜色相同，问有多少种涂法．考点：排列、组合的实际应用
专题：应用题,排列组合
分析：先考虑图形中的3，5，7，再考虑2、4，从而可确定左上角1的涂法，同理可得右下角9的涂法，利用乘法原理，可得结论．
解答：
解：这个问题可分为三步，第一步涂3，5，7，有3种可能，当3，5，7为其中一种颜色时，
第二步涂1、4、2，先考虑2、4就只有两种可能，再考虑1．
如果2、4颜色相同的两种情况下，为另外两种颜色，每取一种颜色，1各有2种，
故1、4、2的涂法就有2×2=4种可能．
若2、4颜色不同，则只有一种可能，加之2、4排列不同，2种．于是左上角1有1种涂法，此时1、4、2的涂法就有2种．
第三步涂8、9、6，同理可得有六种涂法，
根据乘法原理，可得所有涂法共有3×6×6=108种，
第二步涂1、4、2，先考虑2、4就只有两种可能，再考虑1．
如果2、4颜色相同的两种情况下，为另外两种颜色，每取一种颜色，1各有2种，
故1、4、2的涂法就有2×2=4种可能．
若2、4颜色不同，则只有一种可能，加之2、4排列不同，2种．于是左上角1有1种涂法，此时1、4、2的涂法就有2种．
第三步涂8、9、6，同理可得有六种涂法，
根据乘法原理，可得所有涂法共有3×6×6=108种，
点评：本题考查考查乘法原理，考查分类讨论的数学思想，正确分步是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
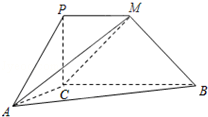如图，PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=PC=AC=1，BC=2，又∠ACB=120°，AB⊥PC．
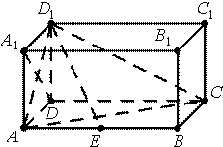如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．
如图，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC，PC的中点．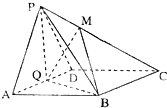
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
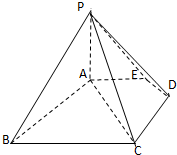如图，五棱锥P-ABCDE中，PA⊥底面ABCDE，AB∥CD，AC∥ED，AE∥CB，∠ABC=45°，