题目内容

在平面直角坐标系xOy中，曲线
4
x2
+
9
y2
=1上的点到原点O的最短距离为
 
．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设曲线
4
x2
+
9
y2
=1上的点P（x，y）．则P（x，y）到原点的距离：d=
x2+y2
=
(x2+y2)(
4
x2
+
9
y2
)
，由此利用均值定理能求出曲线
4
x2
+
9
y2
=1上的点到原点O的最短距离．
解答： 解：设曲线
4
x2
+
9
y2
=1上的点P（x，y）．
设P（x，y）到原点的距离：
d=
x2+y2

=
(x2+y2)(
4
x2
+
9
y2
)

=
13+
4y2
x2
+
9x2
y2

≥
13+2
4y2
x2
•
9x2
y2

=
25
=5，
当且仅当
4y2
x2
=
9x2
y2
时，d取最小值．
∴曲线
4
x2
+
9
y2
=1上的点到原点O的最短距离为5．
故答案为：5．
点评：本题考查曲线上的点到原点距离的最小值的求法，是中档题，解题时要注意均值定理的合理运用．
练习册系列答案
相关题目
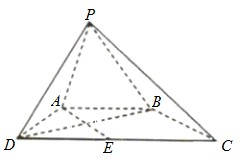如图，在四棱锥P-ABCD中，AB∥CD，△PAB和△PAD是两个边长为2的正三角形．DC=4，PD⊥PB，点E在线段CD上．
（Ⅰ）当
DE
EC
为何值时，AE⊥面PBD：
（Ⅱ）求直线CB与平面PDC所成角的正弦值．
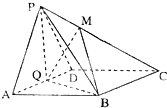如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）点M在线段PC上，PM=
1
3
PC，若平面PAD⊥平面ABCD，且PA=PD=AD=2，求二面角M-BQ-C的大小．
设F1，F2是双曲线C：
x2
16
-
y2
b2
=1(b＞0)的两个焦点，P是双曲线C上一点，若∠F1PF2=90°且△PF1F2的面积为9，则C的离心率为
 
．
设函数f(x)=
x+a
，若函数f（x）=2013x的图象上存在点（x0，y0）使得f（f（y0））=y0，求a的取值范围
 
．
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0），作倾斜角为
π
6
的直线FE交该双曲线右支于点P，若
OE
=
1
2
(
OF
+
OP
)，且
OE
•
EF
=0，则双曲线的离心率为
 
．
若（2x+
a
x
）4（a＞0）的展开式中常数项为96，则实数a等于
 
．
给出下列命题：
（1）若
a
•
b
=
a
•
c
，则
b
=
c
；
（2）对空间任意点O与不共线的三点A，B，C，若
OP
=x
OA
+y
OB
+z
OC
（x，y，z∈R），则P，A，B，C四点共面；
（3）“曲线C上的点的坐标都是方程f（x，y）=0的解”是“曲线C的方程是f（x，y）=0”的必要条件；
（4）（
c
•
b
）
a
-（
a
•
c
）
b
与
c
垂直．
写出以上命题为真命题的序号
 
．
己知某几何体的三视图如图所示，则该几何体的体积是（　　）
A、
2
3
3
+π
B、
2
3
3
+2π
C、2
3
+2π
D、2
3
+π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网