题目内容
已知函数f(x)=ax-
,当x∈(0,4]时,f(x)<0恒成立,求实数a的取值范围.
| 4x-x2 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式f(x)<0恒成立,将参数进行分离,然后求函数的最值即可得到结论.
解答:
解:∵(x)=ax-
,当x∈(0,4]时,f(x)<0恒成立,
∴ax<
,
当x∈(0,4]时,
a<
=
=
,
当x∈(0,4]时,
-1≥0,即
≥0,
∴要使f(x)<0恒成立,
则a<0.
| 4x-x2 |
∴ax<
| 4x-x2 |
当x∈(0,4]时,
a<
| ||
| x |
|
|
当x∈(0,4]时,
| 4 |
| x |
|
∴要使f(x)<0恒成立,
则a<0.
点评:本题主要考查不等式恒成立问题,利用参数分离法是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
执行如图所示的程序框图.若输入x=7,则输出k的值是( )


| A、2 | B、3 | C、4 | D、5 |
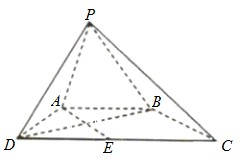 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.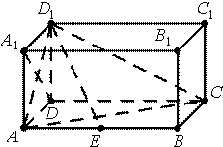 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.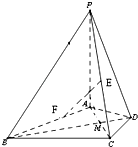 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.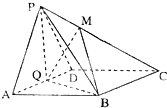 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.