题目内容
已知函数f(x)=x+
,g(x)=x2-bx a、b∈R.
(1)若集合{x|f(x)=2x+2}只含有一个元素,试求实数a的值;
(2)在(1)的条件下,当m∈[2,4],n∈[1,5]时有f(m)大于等于g(n)恒成立,试求实数b的取值范围.
| a |
| x |
(1)若集合{x|f(x)=2x+2}只含有一个元素,试求实数a的值;
(2)在(1)的条件下,当m∈[2,4],n∈[1,5]时有f(m)大于等于g(n)恒成立,试求实数b的取值范围.
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)f(x)=2x+2}转化为x2+2x-a=0,利用根的判别式为0,可求若集合{x|f(x)=2x+2}只含有一个元素,实数a的值;
(2)求出f(m)的最小值,问题转化为n2-bn≤
,n∈[1,5]时恒成立,分离参数求最值,即可求实数b的取值范围.
(2)求出f(m)的最小值,问题转化为n2-bn≤
| 3 |
| 2 |
解答:
解:(1)f(x)=2x+2,即x+
=2x+2,
∴x2+2x-a=0.
∵集合{x|f(x)=2x+2}只含有一个元素,
∴△=4+4a=0,
∴a=-1;
(2)f(m)=m-
,∵m∈[2,4],∴f(m)min=2-
=
,
∵当m∈[2,4],n∈[1,5]时有f(m)大于等于g(n)恒成立,
∴n2-bn≤
,n∈[1,5]时恒成立,
∴b≥n-
,
∵y=n-
,n∈[1,5]时单调递增,
∴b≥1-
=-
.
| a |
| x |
∴x2+2x-a=0.
∵集合{x|f(x)=2x+2}只含有一个元素,
∴△=4+4a=0,
∴a=-1;
(2)f(m)=m-
| 1 |
| m |
| 1 |
| 2 |
| 3 |
| 2 |
∵当m∈[2,4],n∈[1,5]时有f(m)大于等于g(n)恒成立,
∴n2-bn≤
| 3 |
| 2 |
∴b≥n-
| 3 |
| 2n |
∵y=n-
| 3 |
| 2n |
∴b≥1-
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数恒成立问题,考查函数的最值,考查分离参数法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目

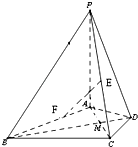 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.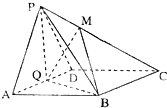 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.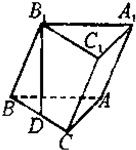 如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.
如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.