题目内容
 如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.
如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.(Ⅰ)试在圆0上找一点D,使得BD与平面PAC平行;
(Ⅱ)二选一:(两题都做,按第一题的解答给分)
①求直线PB与面PAC所成的角的正弦值
②二面角B-PA-C的正弦值.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)D点是C点关于O点的对称点.证明DB∥AC,可得BD与平面PAC平行;
(Ⅱ)①利用VP-ABC=VB-APC,求出dB=
,从而可求直线PB与面PAC所成的角的正弦值;
②取PA中点H,连BH,则BH⊥PA,从而可求二面角B-PA-C的正弦值.
(Ⅱ)①利用VP-ABC=VB-APC,求出dB=
| OP•S△ABC |
| S△PAC |
②取PA中点H,连BH,则BH⊥PA,从而可求二面角B-PA-C的正弦值.
解答:
解:(Ⅰ)D点是C点关于O点的对称点.
证明如下:连DA、DB,由条件可得ABCD是矩形,
则DB∥AC,
因为AC?面PAC,BD?面PAC,
所以BD∥面PAC…(5分)
(Ⅱ)①不妨设OA=R,则PA=PB=PC=2R.
由条件可知PO⊥面ABC,
在△PAC中,PA=PC=2R,AC=
R,则△PAC面积为
R2,
又S△ABC=
|OP|=
R
因为VP-ABC=VB-APC,所以dB=
=
R…(4分)
设直线PB与面PAC所成的角大小为θ,则sinθ=
=
②取PA中点H,连BH,则BH⊥PA…(4分)
设二面角B-PA-C的大小为θ,sinθ=
=
…(4分).
证明如下:连DA、DB,由条件可得ABCD是矩形,
则DB∥AC,
因为AC?面PAC,BD?面PAC,
所以BD∥面PAC…(5分)
(Ⅱ)①不妨设OA=R,则PA=PB=PC=2R.
由条件可知PO⊥面ABC,
在△PAC中,PA=PC=2R,AC=
| 3 |
| ||
| 4 |
又S△ABC=
| ||
| 2 |
| 3 |
因为VP-ABC=VB-APC,所以dB=
| OP•S△ABC |
| S△PAC |
2
| ||
| 13 |
设直线PB与面PAC所成的角大小为θ,则sinθ=
| dB |
| |PB| |
| ||
| 13 |
②取PA中点H,连BH,则BH⊥PA…(4分)
设二面角B-PA-C的大小为θ,sinθ=
| dB |
| |PH| |
2
| ||
| 13 |
点评:本题考查线面平行,考查线面角,面面角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
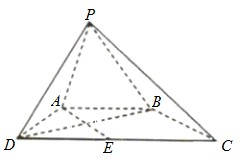 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.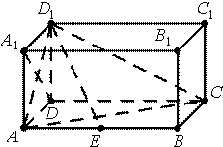 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.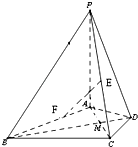 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°. 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.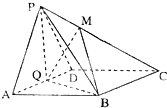 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.