题目内容
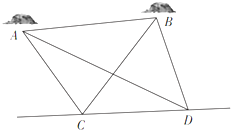 如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)
如图,A,B是海平面上的两个小岛,为测量A,B两岛间的距离,测量船以15海里/小时的速度沿既定直线CD航行,在t1时刻航行到C处,测得∠ACB=75°,∠ACD=120°,1小时后,测量船到达D处,测得∠ADC=30°,∠ADB=45°,求A,B两小岛间的距离.(注:A、B、C、D四点共面)考点:解三角形的实际应用
专题:综合题,解三角形
分析:在在△ACD中,由正弦定理求出AD,在△BCD中,由正弦定理求出BD,在△ABD中,由余弦定理得AB
解答:
解:由已知得CD=15,∠ACD=120°∠ADC=30°,∴∠CAD=30°,
在△ACD中,由正弦定理得
=
,…(2分)
∴AD=15
;…(4分)
∵∠BDC=75°,∠BCD=45°,∴∠CBD=60°,
在△BCD中,由正弦定理得,
=
,…(6分)
∴BD=5
;…(8分)
在△ABD中,∠ADB=45°,由余弦定理得AB=
=5
…(10分)
故两小岛间的距离为5
海里.…(12分)
在△ACD中,由正弦定理得
| 15 |
| sin30° |
| AD |
| sin120° |
∴AD=15
| 3 |
∵∠BDC=75°,∠BCD=45°,∴∠CBD=60°,
在△BCD中,由正弦定理得,
| 15 |
| sin60° |
| BD |
| sin45° |
∴BD=5
| 6 |
在△ABD中,∠ADB=45°,由余弦定理得AB=
(15
|
| 15 |
故两小岛间的距离为5
| 15 |
点评:本题考查利用数学知识解决实际问题,考查正弦定理、余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图.若输入x=7,则输出k的值是( )


| A、2 | B、3 | C、4 | D、5 |

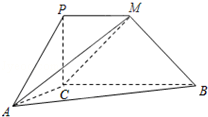 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=PC=AC=1,BC=2,又∠ACB=120°,AB⊥PC.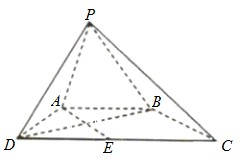 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E在线段CD上.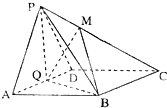 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.