题目内容
已知点
在抛物线C：
的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，则直线BF的斜率为（ ）
A． | B． | C． | D． |
D
解析试题分析：由于点在抛物线C：的准线上，所以
，设直线AB的方程为
，将
与
联立，即
，则
（负值舍去），将k=2代入
得y=8，即可求出x=8，故B（8,8），所以
，故选D.
考点：1.直线与抛物线的位置关系；2.斜率公式.
练习册系列答案
相关题目
与抛物线
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
, 则此双曲线的离心率等于( )．
已知
是直线
被椭圆
所截得的线段的中点，则直线的方程是( )
A． | B． | C． | D． |
如图，
，
，
为两个定点，
是
的一条切线，若过
，
两点的抛物线以直线为准线，则该抛物线的焦点的轨迹是( )
| A．圆 | B．双曲线 | C．椭圆 | D．抛物线 |
已知
为双曲线
:
的一个焦点，则点到的一条渐近线的距离为（ ）
A． | B．3 | C． | D． |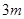
设
、
是关于
的方程
的两个不等实根，则过
，
两点的直线与双曲线
的公共点的个数为（ ）
| A．0 | B．1 | C．2 | D．3 |
以椭圆
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 （ ）
A． | B． | C． | D． |
若抛物线
的焦点与椭圆
的右焦点重合，则
的值为（ ）
A． | B． | C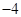． | D． |
已知双曲线
的实轴长为2，则该双曲线的离心率为（ ）
A． | B． | C． | D． |