题目内容
如图, ,
, ,
, 为两个定点,
为两个定点, 是
是 的一条切线,若过
的一条切线,若过 ,
, 两点的抛物线以直线
两点的抛物线以直线 为准线,则该抛物线的焦点的轨迹是( )
为准线,则该抛物线的焦点的轨迹是( )
| A.圆 | B.双曲线 | C.椭圆 | D.抛物线 |
C
解析试题分析:焦点到 和
和 的距离之和等于
的距离之和等于 和
和 分别到准线的距离和,而距离之和为
分别到准线的距离和,而距离之和为 和
和 的中点
的中点 到准线的距离的二倍是定值,结合椭圆的定义得焦点的轨迹方程
到准线的距离的二倍是定值,结合椭圆的定义得焦点的轨迹方程 是以
是以 和
和 为焦点的椭圆.
为焦点的椭圆.
考点:圆锥曲线的轨迹问题.

练习册系列答案
相关题目
设 ,
,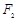 分别是椭圆
分别是椭圆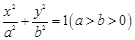 的左、右焦点,过
的左、右焦点,过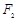 的直线交椭圆于
的直线交椭圆于 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. | B. | C. | D. |
已知双曲线 -
- =1的右焦点为(3,0),则该双曲线的离心率等于( )
=1的右焦点为(3,0),则该双曲线的离心率等于( )
A. | B. | C. | D.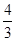 |
设e是椭圆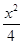 +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( )
| A.(0,3) | B.(3, ) ) |
C.(0,3)∪( ,+∞) ,+∞) | D.(0,2) |

 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )



 在抛物线C:
在抛物线C: 的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )
的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )




 的左、右焦点为
的左、右焦点为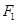 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若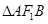 的周长为
的周长为 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.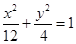
 ,椭圆
,椭圆 的方程为
的方程为 ,双曲线
,双曲线 的方程为
的方程为 ,
, ,则
,则


 ,4),则|PA|+|PM|的最小值是( )
,4),则|PA|+|PM|的最小值是( )