题目内容
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C.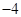 | D. |
D
解析试题分析:由椭圆方程可知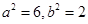 ,所以
,所以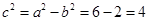 ,即
,即 。所以椭圆右焦点为
。所以椭圆右焦点为 。即抛物线的焦点为
。即抛物线的焦点为 ,可知
,可知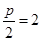 ,解得
,解得 。故D正确。
。故D正确。
考点:椭圆及抛物线的方程和简单几何性质。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知双曲线 -
- =1的右焦点为(3,0),则该双曲线的离心率等于( )
=1的右焦点为(3,0),则该双曲线的离心率等于( )
A. | B. | C. | D.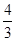 |
设椭圆的方程为 右焦点为
右焦点为 ,方程
,方程 的两实根分别为
的两实根分别为 ,则
,则 ( )
( )
A.必在圆 内 内 |
B.必在圆 外 外 |
C.必在圆 外 外 |
D.必在圆 与圆 与圆 形成的圆环之间 形成的圆环之间 |
[2013·天津高考]已知双曲线 -
- =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 ,则p=( )
,则p=( )
| A.1 | B. | C.2 | D.3 |
方程mx2+y2=1所表示的所有可能的曲线是( )
| A.椭圆、双曲线、圆 |
| B.椭圆、双曲线、抛物线 |
| C.两条直线、椭圆、圆、双曲线 |
| D.两条直线、椭圆、圆、双曲线、抛物线 |
 在抛物线C:
在抛物线C: 的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )
的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )




 的左、右焦点为
的左、右焦点为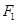 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若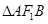 的周长为
的周长为 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.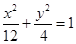
 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
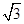


 ,4),则|PA|+|PM|的最小值是( )
,4),则|PA|+|PM|的最小值是( )