题目内容
若函数y=f（x）的图象上任意一点P（x，y）满足条件|x|≤|y|，则称函数f（x）为“优雅型”函数．下列函数中为“优雅型”函数的是（ ）
| A、f（x）=ln（|x|+1） | ||
| B、f（x）=sinx | ||
| C、f（x）=tanx | ||
D、f（x）=x+
|
考点：利用导数研究曲线上某点切线方程
专题：计算题,函数的性质及应用
分析：根据“优雅型”函数的定义，通过特殊值法进行排除即可．
解答：
解：对于A，x=e-1，则y=1，不满足；
对于B，x=
，y=1，不满足；
对于C，x=
，y=1，不满足，
对于D，曲线的两条渐近线为y轴与y=x，符合题意，
故选：D
对于B，x=
| π |
| 2 |
对于C，x=
| 5π |
| 4 |
对于D，曲线的两条渐近线为y轴与y=x，符合题意，
故选：D
点评：本题主要考查与函数有关的新定义题，正确理解题意是解决本题的关键，通过特殊值法进行排除．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
若函数f（x）=-a•2x与f（x）=4x+a+1的图象有交点，则a的取值范围是（ ）
A、a≤2-2
| ||||
| B、a＜-1 | ||||
C、-1≤a≤2-2
| ||||
D、a≤2-2
|
已知定义在R上的函数f（x）满足f（1）=1，且f（x）的导数f′（x）在R上恒有f′（x）＜
，则不等式f（x）＜
x+
的解集为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、（1，+∞） |
| B、（-∞，-1） |
| C、（-1，1） |
| D、（-∞，-1）∪（1，+∞） |
储油30m3的油桶，每分钟流出
m3的油，则桶内剩余油量Q（m3）以流出时间t（分）为自变量的函数的定义域为（ ）
| 3 |
| 4 |
| A、[0，+∞） | ||
B、[0，
| ||
| C、（-∞，40] | ||
| D、[0，40] |
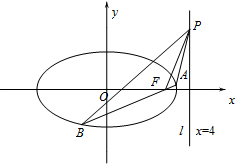如图：椭圆C：