Question

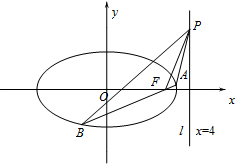如图：椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率e=

1

2

，椭圆上点到直线l：x=4的最短距离为2．
（1）求椭圆C的方程；
（2）AB是经过右焦点F的任一弦，P是直线l上的任意点，记PA，PF，PB的斜率分别为k₁，k₂，k₃．问：是否存在常数λ，使得k₁+k₃=λk₂？若存在，求λ的值；若不存在，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题

分析：求椭圆C的方程即确定a，b，c；设出直线AB的方程并与椭圆方程联立，用韦达定理化简，求出λ的值．

解答： 解：（1）由题意得4-a=2，∴a=2
∵e=

c

a

=

1

2

，∴c=1，b²=3；
∴椭圆C的方程为：

x2

4

+

y2

3

=1．
（2）设P（4，m），直线AB的方程为x=ty+1；
代入

x2

4

+

y2

3

=1消去x化简得，
（3t²+4）y²+6ty-9=0
设A（x₁，y₁），B（x₂，y₂）
则由韦达定理知，y1+y2=-

6t

3t2+4

 ，y1y2=-

9

3t2+4

；
∴k1+k3=

y1-m

x1-4

+

y2-m

x2-4

=

y1-m

ty1-3

+

y2-m

ty2-3

=

(y1-m)(ty2-3)+(y2-m)(ty1-3)

(ty1-3)(ty2-3)

=

2ty1y2-(3+mt)(y1+y2)+6m

t2y1y2-3t(y1+y2)+9

=

2

3

m
又∵k2=

m

4-1

=

m

3

∴k₁+k₃=2k₂，
则λ=2．

点评：本题第一问比较简单，第2问要注意借助韦达定理简化运算．