题目内容
已知函数f(x)=ax3+x2+bx(a、b为常数),g(x)=f(x)+f′(x)是奇函数.
(1)求f(x)的表达式;
(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值、最小值.
解 (1)由已知,f′(x)=3ax2+2x+b,
因此g(x)=f(x)+f′(x)=ax3+(3a+1)x2+(b+2)x+b.
∵g(x)为奇函数.∴g(-x)=-g(x).
 ∴f(x)=-
∴f(x)=- x3+x2.
x3+x2.
(2)由(1)知g(x)=- x3+2x,
x3+2x,
∴g′(x)=-x2+2.
令g′(x)=0,
解得x1=- ,x2=
,x2= ,
,
∴当x∈(-∞,- ),(
),( ,+∞)时,g(x)单调递减,
,+∞)时,g(x)单调递减,
当x∈(- ,
, )时,g(x)单调递增.
)时,g(x)单调递增.
又g(1)= ,g(
,g( )=
)= ,g(2)=
,g(2)= ,
,
∴g(x)在区间[1,2]上的最大值为g( )=
)= ,
,
最小值为g(2)= .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f(x)的定义域是[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 1.5 | 2 | 1 |

下列关于函数f(x)的命题:
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a最多有4个零点.
其中正确命题的序号是________.
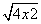 关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是________.
关于f(x)=3x+b的“对称函数”,且h(x)>g(x)恒成立,则实数b的取值范围是________.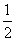 x2-cosx,x∈[-1,1],则导函数f′(x)是( )
x2-cosx,x∈[-1,1],则导函数f′(x)是( ) f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数: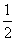 x,g(x)=cos
x,g(x)=cos =
= ,则cos
,则cos =________.
=________.