题目内容
若函数f(x),g(x)满足 f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
①f(x)=sin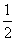 x,g(x)=cos
x,g(x)=cos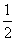 x;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.
x;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.
其中为区间[-1,1]上的正交函数的组数是( )
A.0 B.1
C.2 D.3
C解析 对于①, sin
sin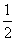 x·cos
x·cos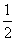 xdx
xdx


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
若函数f(x),g(x)满足 f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
①f(x)=sin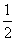 x,g(x)=cos
x,g(x)=cos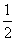 x;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.
x;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.
其中为区间[-1,1]上的正交函数的组数是( )
A.0 B.1
C.2 D.3
C解析 对于①, sin
sin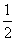 x·cos
x·cos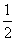 xdx
xdx


 名校课堂系列答案
名校课堂系列答案