题目内容
已知函数f(x)＝x3＋(1－a)x2－a(a＋2)x＋b(a，b∈R)．
(1)若函数f(x)的图象过原点，且在原点处的切线斜率为－3，求a，b的值．
(2)若曲线y＝f(x)存在两条垂直于y轴的切线，求a的取值范围．
解 f′(x)＝3x2＋2(1－a)x－a(a＋2)．
(1)由题意得
解得b＝0，a＝－3或1.
(2)∵曲线y＝f(x)存在两条垂直于y轴的切线，
∴关于x的方程f′(x)＝3x2＋2(1－a)x－a(a＋2)＝0有两个不相等的实数根，
∴Δ＝4(1－a)2＋12a(a＋2)>0，
即4a2＋4a＋1>0.∴a≠－
.
∴a的取值范围是
练习册系列答案
相关题目
.
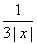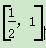恒成立，求m的取值范围．
A．y＝
x3－
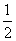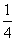x3－x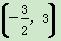
B．(0，－4)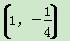
x3－
x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．
)(x≠0)，且cosα＝
x，求sinα、tanα的值．