题目内容
若两个三角形不在同一平面内，它们的边两两对应平行，那么这两个三角形（ ）
| A、全等 | B、相似 |
| C、仅有一个角相等 | D、全等或相似 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：由等角定理得这两个三角形的三组对应角分别相等，所以这两个三角形全等或相似．
解答：
解：在△ABC和△A1B1C1中，
∵AB∥A1B1，AC∥A1C1，∴∠BAC=∠B1A1C1，
同理可证：∠ABC=∠A1B1C1，
∠ACB=∠A1C1B1，
∴△ABC∽△A1B1C1或△ABC≌△A1B1C1．
故选：D．
∵AB∥A1B1，AC∥A1C1，∴∠BAC=∠B1A1C1，
同理可证：∠ABC=∠A1B1C1，
∠ACB=∠A1C1B1，
∴△ABC∽△A1B1C1或△ABC≌△A1B1C1．
故选：D．
点评：本题考查两个三角形是否相似的判断，是基础题，解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用．
练习册系列答案
相关题目
一几何体的正视图和侧视图是边长为2的等边三角形，俯视图是直径为2的圆，则此几何体的表面积为（ ）
A、4π+2
| ||
B、2π+2
| ||
| C、3π | ||
| D、2π |
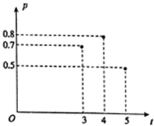加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足下列某函数关系：①p=at+b②p=alogbt③p=at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，
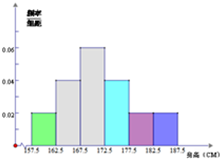云南省2014年全省高中男生身高统计调查数据显示：全省100000名男生的身高服从正态分布N（107.5，16）．现从我校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于157.5cm和187.5cm之间，将测量结果按如下方式分成6组：第一组[157.5，162.5]，第二组[162.5，167.5]，…，第6组[182.5，187.5]，如图是按上述分组方法得到的频率分布直方图．