题目内容
在四棱锥A-BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B-AE-C的余弦值.
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B-AE-C的余弦值.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)设BE的中点为O,连结AO,DO,由已知得AO⊥BE,DO⊥BE,从而AO⊥平面BCDE,设AB=1,以B为原点,以BC为x轴,BD为y轴,建立空间直角坐标系,利用向量法能求出异面直线AB与DE所成角为60°.
(2)求出平面ACE的法向量和平面ABE的法向量,由此利用向量法能求出二面角B-AE-C的余弦值.
(2)求出平面ACE的法向量和平面ABE的法向量,由此利用向量法能求出二面角B-AE-C的余弦值.
解答:
解:(1)设BE的中点为O,连结AO,DO,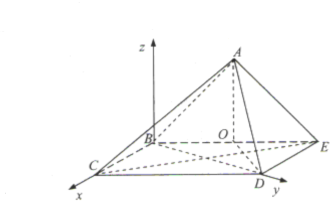
∵AB=AE,BO=OE,∴AO⊥BE,同理DO⊥BE,
又∵平面ABE⊥平面BCDE,
平面ABE∩平面BCDE=BE,
∴AO⊥平面BCDE,
由题意,BE2=2AB2=2DB2,
∴AB=BD=DE=AE,
设AB=1,以B为原点,以BC为x轴,BD为y轴,
建立如图所示的空间直角坐标系,
则B(0,0,0),C(1,0,0),D(0,1,0),
E(-1,1,0),A(-
,
,
),
则
=(
,-
,-
),
=(-1,0,0),
∵cos<
,
>=
=
=-
,
∴
与
的夹角为120°,
异面直线AB与DE所成角为60°.
(2)设平面ACE的法向量
=(x,y,z),
=(
,-
,-
),
=(-1,1,0),
则
,取x=1,得
=(1,1,0),
设平面ABE的法向量为
=(a,b,c),
=(
,-
,
),
=(2,-1,0),
则
,取a=1,得
=(1,2,
),
设二面角B-AE-C的平面角为θ,
cosθ=|cos<
,
>|=
=
=
.
∴二面角B-AE-C的余弦值为
.

∵AB=AE,BO=OE,∴AO⊥BE,同理DO⊥BE,
又∵平面ABE⊥平面BCDE,
平面ABE∩平面BCDE=BE,
∴AO⊥平面BCDE,
由题意,BE2=2AB2=2DB2,
∴AB=BD=DE=AE,
设AB=1,以B为原点,以BC为x轴,BD为y轴,
建立如图所示的空间直角坐标系,
则B(0,0,0),C(1,0,0),D(0,1,0),
E(-1,1,0),A(-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
则
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| DE |
∵cos<
| AB |
| DE |
| ||||
|
|
-
| ||||||||
|
| 1 |
| 2 |
∴
| AB |
| DE |
异面直线AB与DE所成角为60°.
(2)设平面ACE的法向量
| n |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| BE |
则
|
| n |
设平面ABE的法向量为
| m |
| EA |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| EC |
则
|
| m |
| ||
| 2 |
设二面角B-AE-C的平面角为θ,
cosθ=|cos<
| n |
| m |
|
| ||||
|
|
| 3 | ||
|
3
| ||
| 11 |
∴二面角B-AE-C的余弦值为
3
| ||
| 11 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线线角、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
| A、使用了归纳推理 |
| B、使用了类比推理 |
| C、使用了“三段论”,但推理形式错误 |
| D、使用了“三段论”,但小前提错误 |
若直线y=a与函数y=sinx的图象相交,则相邻的两交点间的距离的最大值为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
| A、全等 | B、相似 |
| C、仅有一个角相等 | D、全等或相似 |
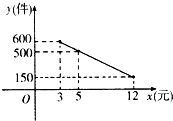 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.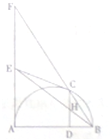 如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.
如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.