题目内容
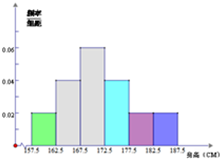 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.(Ⅰ)试评估我校高三年级男生在全省高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(Ⅲ)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人
中身高排名(从高到低)在全省前130名的人数记为ξ,求ξ的数学期望.
参考数据:
若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,
P(μ-3σ<ξ≤μ+3σ)=0.9974.
考点:频率分布直方图,离散型随机变量的期望与方差,正态分布曲线的特点及曲线所表示的意义
专题:概率与统计
分析:(I)计算平均身高用组中值×频率,即可得到结论;
(II)先理解频率分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即每组中包含个体的个数;
根据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出这50名男生身高在177.5cm以上(含177.5cm)的人数;
(III)先根据正态分布的规律求出全市前130名的身高在182.5cm以上的50人中的人数,确定ξ的可能取值,求出其概率,即可得到ξ的分布列与期望.
(II)先理解频率分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即每组中包含个体的个数;
根据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出这50名男生身高在177.5cm以上(含177.5cm)的人数;
(III)先根据正态分布的规律求出全市前130名的身高在182.5cm以上的50人中的人数,确定ξ的可能取值,求出其概率,即可得到ξ的分布列与期望.
解答:
解:(Ⅰ)根据频率分布直方图,得;
我校高三年级男生平均身高为
=160×0.02×5+165×0.04×5+170×0.06×5
+175×0.04×5+180×0.02×5+185×0.02×5=171.5,
∴高于全市的平均值170.5;(4分)
(Ⅱ)由频率分布直方图知,后两组频率为0.2,
∴人数为0.2×50=10,
即这50名男生身高在177.5cm以上(含177.5 cm)的人数为10人;…(6分)
(Ⅲ)∵P(170.5-3×4<ξ≤170.5+3×4)=0.9974,
∴P(ξ≥182.5)=
=0.0013,
∴0.0013×100 000=130,
全省前130名的身高在182.5 cm以上,这50人中182.5 cm以上的有5人;
∴随机变量ξ可取0,1,2,于是
P(ξ=0)=
=
=
,P(ξ=1)=
=
=
,P(ξ=2)=
=
=
,
∴Eξ=0×
+1×
+2×
=1.…(12分)
我校高三年级男生平均身高为
. |
| x |
+175×0.04×5+180×0.02×5+185×0.02×5=171.5,
∴高于全市的平均值170.5;(4分)
(Ⅱ)由频率分布直方图知,后两组频率为0.2,
∴人数为0.2×50=10,
即这50名男生身高在177.5cm以上(含177.5 cm)的人数为10人;…(6分)
(Ⅲ)∵P(170.5-3×4<ξ≤170.5+3×4)=0.9974,
∴P(ξ≥182.5)=
| 1-0.9974 |
| 2 |
∴0.0013×100 000=130,
全省前130名的身高在182.5 cm以上,这50人中182.5 cm以上的有5人;
∴随机变量ξ可取0,1,2,于是
P(ξ=0)=
| ||
|
| 10 |
| 45 |
| 2 |
| 9 |
| ||||
|
| 25 |
| 45 |
| 5 |
| 9 |
| ||
|
| 10 |
| 45 |
| 2 |
| 9 |
∴Eξ=0×
| 2 |
| 9 |
| 5 |
| 9 |
| 2 |
| 9 |
点评:本题考查了频率分布直方图的应用问题,也考查了离散型随机变量的期望与方差的计算问题,是基础题目.

练习册系列答案
相关题目
若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
| A、全等 | B、相似 |
| C、仅有一个角相等 | D、全等或相似 |
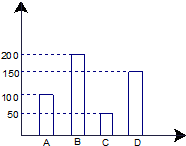 某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.
某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.