题目内容
已知函数f(x)对任意x,y∈R,f(x+y)=f(x)+f(y),且当x>0时,f(x)>0
(1)求f(0)的值;
(2)判断函数f(x)的奇偶性
(3)若已知f(1)=2,试判断函数f(x)的单调性,并求满足f(2-a)=6的实数a的值.
(1)求f(0)的值;
(2)判断函数f(x)的奇偶性
(3)若已知f(1)=2,试判断函数f(x)的单调性,并求满足f(2-a)=6的实数a的值.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)取x=y=0即可求得f(0)的值;
(2)令y=-x,易得f(x)+f(-x)=0,从而可判断其奇偶性;
(3)设x1,x2∈R且x1<x2,作差f(x2)-f(x1)后判断其符号即可证得f(x)为R上的增函数,根据抽象函数的关系求出f(3)=6,然后将方程进行转化即可得到结论.
(2)令y=-x,易得f(x)+f(-x)=0,从而可判断其奇偶性;
(3)设x1,x2∈R且x1<x2,作差f(x2)-f(x1)后判断其符号即可证得f(x)为R上的增函数,根据抽象函数的关系求出f(3)=6,然后将方程进行转化即可得到结论.
解答:
解:(1)取x=y=0得,则f(0+0)=f(0)+f(0),即f(0)=0;
(2)函数f(x)为奇函数,
证明:已知函数的定义域为R,
取y=-x代入,得f(0)=f(x)+f(-x),
又f(0)=0,于是f(-x)=-f(x),
∴f(x)为奇函数;
(3)设x1,x2∈R且x1<x2,
则f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1),
由x2-x1>0知,f(x2-x1)>0,
∴f(x2)>f(x1),
∴函数f(x)为R上的增函数.
若f(1)=2,则f(2)=f(1+1)=f(1)+f(1)=2+2=4,
f(3)=f(2+1)=f(2)+f(1)=4+2=6,
则方程f(2-a)=6等价为f(2-a)=f(3),
∵函数f(x)为R上的增函数,
∴2-a=3,
解得a=-1.
(2)函数f(x)为奇函数,
证明:已知函数的定义域为R,
取y=-x代入,得f(0)=f(x)+f(-x),
又f(0)=0,于是f(-x)=-f(x),
∴f(x)为奇函数;
(3)设x1,x2∈R且x1<x2,
则f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1),
由x2-x1>0知,f(x2-x1)>0,
∴f(x2)>f(x1),
∴函数f(x)为R上的增函数.
若f(1)=2,则f(2)=f(1+1)=f(1)+f(1)=2+2=4,
f(3)=f(2+1)=f(2)+f(1)=4+2=6,
则方程f(2-a)=6等价为f(2-a)=f(3),
∵函数f(x)为R上的增函数,
∴2-a=3,
解得a=-1.
点评:本题考查抽象函数及其应用,以及函数奇偶性和单调性的判断,利用赋值法以及函数奇偶性和单调性的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )
| A、全等 | B、相似 |
| C、仅有一个角相等 | D、全等或相似 |
 已知椭圆C:
已知椭圆C: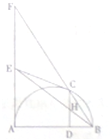 如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.
如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.