题目内容
已知椭圆C:
+
=1(a>b>0)的短轴长为2,离心率为
.过点M(2,0)的直线l与椭圆C相交于A、B两点,O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
•
的取值范围;
(Ⅲ)若B点关于x轴的对称点是N,证明:直线AN恒过一定点.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
| OA |
| OB |
(Ⅲ)若B点关于x轴的对称点是N,证明:直线AN恒过一定点.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆C:
+
=1(a>b>0)的短轴长为2,离心率为
,求出a,b,即可求椭圆C的方程;
(Ⅱ)设l:y=k(x-2),与椭圆C的方程联立,消去y,利用韦达定理,结合数量积公式,即可求
•
的取值范围;
(Ⅲ)由对称性可知N(x2,-y2),定点在x轴上.直线AN:y-y1=
(x-x1),令y=0,即可得出结论.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅱ)设l:y=k(x-2),与椭圆C的方程联立,消去y,利用韦达定理,结合数量积公式,即可求
| OA |
| OB |
(Ⅲ)由对称性可知N(x2,-y2),定点在x轴上.直线AN:y-y1=
| y1+y2 |
| x1-x2 |
解答:
(Ⅰ)解:由题意b=1,e=
=
得a2=2c2=2a2-2b2,故a2=2.
故方程为
+y2=1.(3分)
(Ⅱ)解:设l:y=k(x-2),与椭圆C的方程联立,消去y得(1+2k2)x2-8k2x+8k2-2=0.
由△>0得0≤k2<
.
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
.
∴
•
=x1x2+y1y2=x1x2+k2(x1-2)(x2-2)=(1+k2)x1x2-2k2(x1+x2)+4k2
=
=5-
.
∵0≤k2<
,∴
<
≤7,
故所求范围是[-2,
).(8分)
(Ⅲ)证明:由对称性可知N(x2,-y2),定点在x轴上.
直线AN:y-y1=
(x-x1),令y=0得:x=x1-
=
=
=
=1,
∴直线l过定点(1,0).(13分)
| c |
| a |
| ||
| 2 |
故方程为
| x2 |
| 2 |
(Ⅱ)解:设l:y=k(x-2),与椭圆C的方程联立,消去y得(1+2k2)x2-8k2x+8k2-2=0.
由△>0得0≤k2<
| 1 |
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
∴
| OA |
| OB |
=
| 10k2-2 |
| 1+2k2 |
| 7 |
| 1+2k2 |
∵0≤k2<
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 1+2k2 |
故所求范围是[-2,
| 3 |
| 2 |
(Ⅲ)证明:由对称性可知N(x2,-y2),定点在x轴上.
直线AN:y-y1=
| y1+y2 |
| x1-x2 |
| y1(x1-x2) |
| y1+y2 |
| x1y2+x2y1 |
| y1+y2 |
| 2x1x2-2(x1+x2) |
| x1+x2-4 |
| ||||
|
∴直线l过定点(1,0).(13分)
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量的数量积,考查韦达定理,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.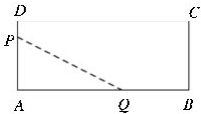 如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为
如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为