Question

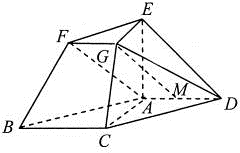
在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB=90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC，AB=2EF．
（1）若M是线段AD的中点，求证：GM∥平面ABFE；
（2）若AC=BC=2AE=2，求二面角A-BF-C的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面平行的判定

专题：空间角

分析：（1）由已知条件推导出∠EGF=90°，△ABC∽△EFG，连结AF，推导出四边形AFGM为平行四边形，由此能证明GM∥平面ABFE．
（2）分别以AC，AD，AE所在直线为x轴、y轴、z轴，建立空间直角坐标系A-xyz，利用向量法能求出二面角A-BF-C的余弦值．

解答： （1）证明：∵EF∥AB，FG∥BC，EG∥AC，∠ACB=90°，
∴∠EGF=90°，△ABC∽△EFG．…．（2分）
∵AB=2EF，∴BC=2FG，
连结AF，FG∥BC，FG=

1

2

BC，…．（3分）
在平行四边形ABCD中，M是线段AD的中点，
∴AM∥BC，且AM=

1

2

BC，…．（4分）
∴FG∥AM，且FG=AM，
∴四边形AFGM为平行四边形，∴GM∥FA，
又FA?平面ABFE，GM不包含于平面ABFE，
∴GM∥平面ABFE．…（6分）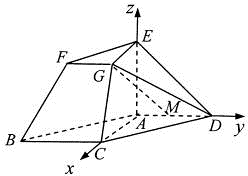
（2）解：∵∠ACB=90°，∴∠ACD=90°，
又EA⊥平面ABCD，∴AC，AD，AE两两垂直．
分别以AC，AD，AE所在直线为x轴、y轴、z轴，
建立如图所示的空间直角坐标系A-xyz．…．（7分）
则由题意知A（0，0，0），B（2，-2，0），
C（2，0，0），D（0，0，1）…．（8分）
∴

AB

=（2，-2，0），

BC

=（0，2，0），
又EF=

1

2

AB，∴F（1，-1，1），

BF

=（-1，1，1）．
设平面BFC的法向量

m

=（x，y，z），
则

m • BC =2y=0 m • BF =-x+y+z=0

，
取x=1，得

m

=（1，0，1）…．（10分）
设平面ABF的法向量

n

=（x₁，y₁，z₁），
则

n • AB =2x1-2y1=0 n • BF =-x1+y1+z1=0

，
取x₁=1，得

n

=（1，1，0）．…．（12分）
∴cos＜

m

，

n

＞=

1

2 • 2

=

1

2

，
故二面角A-BF-C的余弦值为

1

2

．…．（14分）

点评：本题考查直线与平面平行的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．