Question

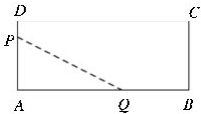如图，有一矩形地块ABCD，其相邻边长为20m和50m，现要在它的短边与长边上各取一点P与Q，用周长为80m的篱笆围出一块直角三角形的花园，则围出部分的最大面积为

 

m²．

Answer 1

考点：基本不等式

专题：不等式的解法及应用

分析：分类讨论：①周长为80一定，设AP=a，AQ=b，则PQ=

a2+b2

．（0＜a≤20，0＜b≤50）．
可得a+b+

a2+b2

=80，利用基本不等式可知：此时不符合题意．
②当AP=a取最大20时，AQ=b，则斜边60-b，利用勾股定理可得b²+20²=（60-b）²，解出即可．

解答： 解：①周长为80一定，设AP=a，AQ=b，则PQ=

a2+b2

．（0＜a≤20，0＜b≤50）．
∴a+b+

a2+b2

=80，
∴80≥2

ab

+

2ab

，当且仅当a=b=40(2-

2

)＞20取等号，
而此时a＞20，不符合题意，应舍去．
②当AP=a取最大20时，AQ=b，则斜边60-b，
由勾股定理可得b²+20²=（60-b）²，
解得b=

80

3

＜50，满足条件．
此时直角△APQ取得最大值：S=

1

2

×20×

80

3

=

800

3

．
综上可知：围出部分的最大面积为

800

3

．
故答案为：

800

3

．

点评：本题考查了分类讨论的方法、基本不等式的性质、勾股定理、三角形的面积等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．