题目内容
一条长椅上有7个座位,4个人坐,还有3个空位子,求:
(1)至少有两人坐在一起,有多少种不同的坐法?
(2)三个空位都不相邻,有多少种不同的坐法?
(1)至少有两人坐在一起,有多少种不同的坐法?
(2)三个空位都不相邻,有多少种不同的坐法?
考点:计数原理的应用
专题:排列组合
分析:(1)利用间接法,没有限制的坐法
=840种,其中4个任都不相邻的有
=24种,问题得以解决;
(2)利用间接法,没有限制的坐法
=840种,其中三个空位都相邻的有
=120种,问题得以解决.
| A | 4 7 |
| A | 4 4 |
(2)利用间接法,没有限制的坐法
| A | 4 7 |
| A | 5 5 |
解答:
解:(1)利用间接法,没有限制的坐法
=840种,其中4个任都不相邻的有
=24种,故至少有两人坐在一起,有840-24=816种不同的坐法;
(2)利用间接法,没有限制的坐法
=840种,其中三个空位都相邻的有
=120种,故三个空位都不相邻,有840-120=720种不同的坐法.
| A | 4 7 |
| A | 4 4 |
(2)利用间接法,没有限制的坐法
| A | 4 7 |
| A | 5 5 |
点评:本题主要考查用排列组合及简单的计数原理问题间接法是解决题目的关键,有一定的灵活性,需要同学们很好的理解,属于中档题.

练习册系列答案
相关题目
 在长方体ABCD-A1B1C1D1中,AD=AB=
在长方体ABCD-A1B1C1D1中,AD=AB=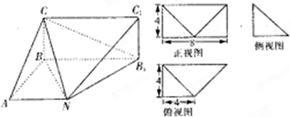 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角表,俯视图为直角梯形.