题目内容
函数f（x）=x2+2（a-1）x+2在区间[-1，4]上为减函数，则a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据二次函数的单调性，f（x）在（-∞，1-a]上单调递减，所以4≤1-a，从而得出a的取值范围．
解答：
解：二次函数f（x）的对称轴是：x=1-a；
根据二次函数的单调性知f（x）在（-∞，1-a]上单调递减；
∴[-1，4]⊆（-∞，1-a]
∴4≤1-a
∴a≤-3．
∴a的取值范围是：（-∞，-3]．
故答案是：（-∞，-3]．
根据二次函数的单调性知f（x）在（-∞，1-a]上单调递减；
∴[-1，4]⊆（-∞，1-a]
∴4≤1-a
∴a≤-3．
∴a的取值范围是：（-∞，-3]．
故答案是：（-∞，-3]．
点评：能掌握二次函数的单调性，及单调区间是求解本题的关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
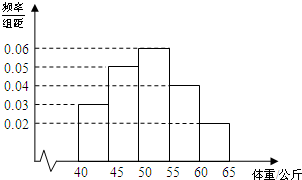某校高三年级共1200人．学校为了检查同学们的健康状况，随机抽取了高三年级的100名同学作为样本，测量他们的体重（单位：公斤），体重的分组区间为[40，45），[45，50），[50，55），（55，60），[60，65]，由此得到样本的频率分布直方图，如图．根据频率分布直方图，估计该校高三年级体重低于50公斤的人数为