题目内容
在△ABC中，A：B：C=1：2：3，则sinA：sinB：sinC=（ ）
| A、1：2：3 | ||||
B、1：
| ||||
C、1：
| ||||
D、1：
|
考点：三角函数的化简求值
专题：三角函数的求值,解三角形
分析：依题意，可求得A=
，B=
，C=
，利用特殊角的三角函数值即可求得答案．
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
解答：
解：在△ABC中，A：B：C=1：2：3，
∴A=
，B=
，C=
，
∴sinA：sinB：sinC=sin
：sin
：sin
=
：
：1=1：
：2；
故选：D．
∴A=
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
∴sinA：sinB：sinC=sin
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故选：D．
点评：本题考查解三角形，依题意，求得A=
，B=
，C=
是关键，考查比例关系的应用与特殊角的三角函数值，考查运算能力，属于中档题．
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
化简
的结果是（ ）
| 1-sin260° |
| A、cos60° |
| B、-cos60° |
| C、±cos60° |
| D、±|cos60°| |
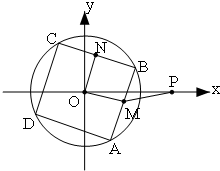如图，已知点P（2，0），正方形ABCD内接于⊙O：x2+y2=2，M、N分别为边AB、BC的中点，当正方形ABCD绕圆心O旋转时，| PM |
| ON |
| A、[-1，1] | ||||||||
B、[-
| ||||||||
| C、[-2，2] | ||||||||
D、[-
|
函数y=-sin2x-3cosx+3的最小值是（ ）
| A、2 | ||
| B、0 | ||
C、
| ||
| D、6 |
已知α=2，则点P（sinα，tanα）所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
从高三年级随机抽取100名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由图中数据可知成绩在[130，140）内的学生人数为（ ）| A、20 | B、25 | C、30 | D、35 |
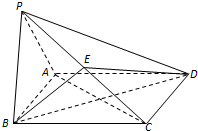如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC，E为PC的中点．