��Ŀ����
3����֪$\overrightarrow{a}$��$\overrightarrow{b}$Ϊ��������������������p��|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|������q��$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ�������p������q�����ģ�������| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
���� ��$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ�ȣ���$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ���cos��=��1���������������������ʼ����жϳ����ۣ�
��� �⣺��$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ�ȣ�
��$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ���cos��=��1��
��|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$||cos��|=|$\overrightarrow{a}$||$\overrightarrow{b}$|��
��֮Ҳ������
������p������q�����ij�Ҫ������
��ѡ��C��
���� ���⿼���������������������ʡ��������߶��������������ж�������������������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
13��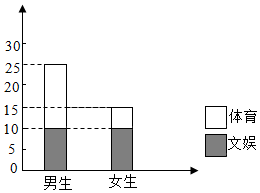 ��ij��ѧ���ǰ����������ǰ���������е��飬���ݵ���õ������ݣ������ƵĶ�ά����ͼ��ͼ��
��ij��ѧ���ǰ����������ǰ���������е��飬���ݵ���õ������ݣ������ƵĶ�ά����ͼ��ͼ��
��1������ͼ�����ݣ�����2��2��������
��2����Ҫ���÷ֲ�����ķ����������й���ȡ5����ѡ�ˣ��ٴ�5����ѡ���˷ֱ�������Э���ˣ���ѡ��������ǡ����һ�˸��������飬��һ�˸�����������ѧ���ĸ��ʣ�
��3���Ƿ������Ϊ�Ա����Ƿ������й�ϵ��
�ο����ݣ�
 ��ij��ѧ���ǰ����������ǰ���������е��飬���ݵ���õ������ݣ������ƵĶ�ά����ͼ��ͼ��
��ij��ѧ���ǰ����������ǰ���������е��飬���ݵ���õ������ݣ������ƵĶ�ά����ͼ��ͼ����1������ͼ�����ݣ�����2��2��������
��2����Ҫ���÷ֲ�����ķ����������й���ȡ5����ѡ�ˣ��ٴ�5����ѡ���˷ֱ�������Э���ˣ���ѡ��������ǡ����һ�˸��������飬��һ�˸�����������ѧ���ĸ��ʣ�
��3���Ƿ������Ϊ�Ա����Ƿ������й�ϵ��
�ο����ݣ�
| P��K2��k�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11����֪����A={3��$\sqrt{a}$}��B={a��b}����A��B={2}����A��B=��������
| A�� | {2��3} | B�� | {3��4} | C�� | {$\sqrt{2}$��2��3} | D�� | {2��3��4} |
18����֪����A={x|x2-6x+5��0}��B={x|y=$\sqrt{x-3}$}��A��B=��������
| A�� | [1��+�ޣ� | B�� | [1��3] | C�� | ��3��5] | D�� | [3��5] |
8����֪���κ���f��x��=ax2+bx+c�ĵ���Ϊf�䣨x����f�䣨0����0�����������ʵ��x����f��x����0����$\frac{f��1��}{{{f^'}��0��}}$��ȡֵ��Χ�ǣ�������
| A�� | $[\frac{3}{2}��+�ޣ�$ | B�� | [2��+�ޣ� | C�� | $[\frac{5}{2}��+�ޣ�$ | D�� | [3��+�ޣ� |
15�����㣺$\int_1^3{��2x-\frac{1}{x^2}}��dx$=��������
| A�� | $\frac{22}{3}$ | B�� | $\frac{26}{3}$ | C�� | $\frac{34}{3}$ | D�� | $-\frac{2}{27}$ |
13������y=sinx��ͼ����ֱ��y=$\frac{1}{2}$x�Ľ������Ϊ��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 3������ |