题目内容
12．在代数式（4x2-2x-5）（1+$\frac{1}{{x}^{2}}$）5的展开式中，常数等于15．分析 （1+$\frac{1}{{x}^{2}}$）5的展开式的通项公式Tr+1=${∁}_{5}^{r}$$（\frac{1}{{x}^{2}}）^{r}$=${∁}_{5}^{r}{x}^{-2r}$．令-2r=-2，-2r=-1，-2r=0，分别解出即可得出．
解答 解：（1+$\frac{1}{{x}^{2}}$）5的展开式的通项公式Tr+1=${∁}_{5}^{r}$$（\frac{1}{{x}^{2}}）^{r}$=${∁}_{5}^{r}{x}^{-2r}$．
令-2r=-2，-2r=-1，-2r=0，
分别解得：r=1，r=$\frac{1}{2}$（舍去），r=0．
∴常数项=4${∁}_{5}^{1}$-5${∁}_{5}^{0}$=20-5=15．
故答案为：15．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
2．已知x，y∈{1，2，3，4，5，6}，且x+y=7，则$y≥\frac{x}{2}$的概率（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{6}$ |
3．已知$\overrightarrow{a}$，$\overrightarrow{b}$为两个非零向量，设命题p：|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|，命题q：$\overrightarrow{a}$与$\overrightarrow{b}$共线，则命题p是命题q成立的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．执行如图的程序框图，则输出的S的值为（ ）
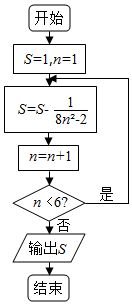
| A． | $\frac{7}{9}$ | B． | $\frac{17}{22}$ | C． | $\frac{10}{13}$ | D． | $\frac{23}{30}$ |