题目内容
8.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意的实数x都有f(x)≥0,则$\frac{f(1)}{{{f^'}(0)}}$的取值范围是( )| A. | $[\frac{3}{2},+∞)$ | B. | [2,+∞) | C. | $[\frac{5}{2},+∞)$ | D. | [3,+∞) |
分析 先根据题目的条件建立关于a、b、c的关系式,再结合基本不等式求出最小即可,注意等号成立的条件.
解答 解:f′(x)=2ax+b,
∴f′(0)=b>0,
∵对于任意的实数x都有f(x)≥0,
∴a≥0,且b2-4ac≤0,
∴b2≤4ac,
∴c>0
∴$\frac{f(1)}{f'(0)}=\frac{a+b+c}{b}=\frac{a+c}{b}+1≥\frac{{2\sqrt{ac}}}{b}+1≥2$,
故选:B.
点评 本题主要考查了导数的运算,以及函数的最值及其几何意义和不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知sin(3π-α)=$\frac{1}{3}$,则cos2α等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
16.设等差数列{an}满足3a8=5a15,且$a_1^{\;}>0$,Sn为其前n项和,则数列{Sn}的最大项为( )
| A. | $S_{23}^{\;}$ | B. | S24 | C. | S25 | D. | S26 |
3.已知$\overrightarrow{a}$,$\overrightarrow{b}$为两个非零向量,设命题p:|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|,命题q:$\overrightarrow{a}$与$\overrightarrow{b}$共线,则命题p是命题q成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.执行如图的程序框图,则输出的S的值为( )
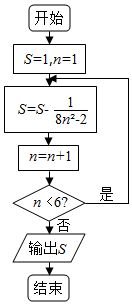

| A. | $\frac{7}{9}$ | B. | $\frac{17}{22}$ | C. | $\frac{10}{13}$ | D. | $\frac{23}{30}$ |
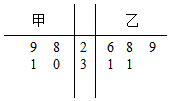 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论: