题目内容
15.计算:$\int_1^3{(2x-\frac{1}{x^2}})dx$=( )| A. | $\frac{22}{3}$ | B. | $\frac{26}{3}$ | C. | $\frac{34}{3}$ | D. | $-\frac{2}{27}$ |
分析 根据定积分的计算法则计算即可.
解答 解:$\int_1^3{(2x-\frac{1}{x^2}})dx$=(x2+$\frac{1}{x}$)|${\;}_{1}^{3}$=(9+$\frac{1}{3}$)-(1+1)=$\frac{22}{3}$,
故选:A.
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6.若f(x)是定义在(-∞,+∞)上的偶函数,?x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}<0$,则( )
| A. | f(3)<f(1)<f(-2) | B. | f(1)<f(-1)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(-2)<f(1) |
3.已知$\overrightarrow{a}$,$\overrightarrow{b}$为两个非零向量,设命题p:|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|,命题q:$\overrightarrow{a}$与$\overrightarrow{b}$共线,则命题p是命题q成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.若tanα=1,则sin2α-cos2α的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
20.执行如图的程序框图,则输出的S的值为( )
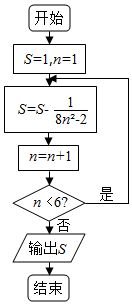

| A. | $\frac{7}{9}$ | B. | $\frac{17}{22}$ | C. | $\frac{10}{13}$ | D. | $\frac{23}{30}$ |
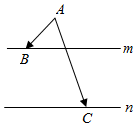 如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.
如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.