题目内容
14.已知向量|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=1,若|$\overrightarrow{a}+2\overrightarrow{b}$|=3,则|$\overrightarrow{b}$|=$\sqrt{3}$.分析 根据题意,由|$\overrightarrow{a}+2\overrightarrow{b}$|=3可得|$\overrightarrow{a}+2\overrightarrow{b}$|2=($\overrightarrow{a}+2\overrightarrow{b}$)2=($\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2)=9,将|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=1代入其中可得$\overrightarrow{b}$2的值,即可得答案.
解答 解:根据题意,若|$\overrightarrow{a}+2\overrightarrow{b}$|=3,
则|$\overrightarrow{a}+2\overrightarrow{b}$|2=($\overrightarrow{a}+2\overrightarrow{b}$)2=($\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2)=9,
而|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=1,
则有$\overrightarrow{b}$2=9-2-4=3,
故|$\overrightarrow{b}$|=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查向量数量积的运算,涉及向量的模的计算,关键是熟练掌握向量数量积的计算公式.

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |

| A. | -1 | B. | 1 | C. | 2 | D. | $\frac{1}{4}$ |
| A. | f(3)<f(1)<f(-2) | B. | f(1)<f(-1)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(-2)<f(1) |
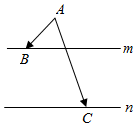 如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.
如图,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B、C分别在m、n上,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=5$,则$\overrightarrow{AB}•\overrightarrow{AC}$的最大值是$\frac{21}{4}$.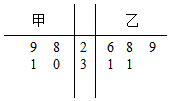 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论: