题目内容
春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:表(一)
表(二)
附:k2=
(1)估计该市居民中,能做到“光盘”行动的居民比例;
(2)判断是否有90%以上的把握认为“该市居民能否做到”光盘”与性别有关?
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(k2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(1)估计该市居民中,能做到“光盘”行动的居民比例;
(2)判断是否有90%以上的把握认为“该市居民能否做到”光盘”与性别有关?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)100名性别不同的居民能做到“光盘”行动的有25名,故可得结论;
(2)代入公式计算k的值,和临界值表比对后即可得到答案.
(2)代入公式计算k的值,和临界值表比对后即可得到答案.
解答:
解:(1)100名性别不同的居民能做到“光盘”行动的有25名,故估计该市居民中,能做到“光盘”行动的居民比例为
=25%;
(2)k2=
≈3.030>2.706,
所以有90%的把握认为“该市居民能否做到”光盘”与性别有关.
| 25 |
| 100 |
(2)k2=
| 100×(45×15-30×10)2 |
| 75×25×55×45 |
所以有90%的把握认为“该市居民能否做到”光盘”与性别有关.
点评:本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
相关题目
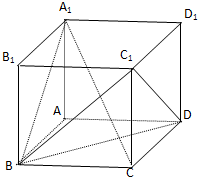 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.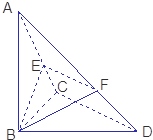 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且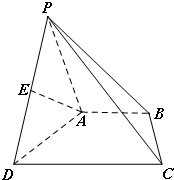 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱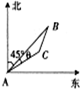 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40