题目内容
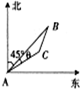 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40| 2 |
| ||
| 6 |
| 3 |
考点:解三角形的实际应用
专题:解三角形
分析:先根据sinθ求得cosθ,进而利用余弦定理求得BC,最后用里程除以时间即可求得其速度.
解答:
解:∵sinθ=
,0°<θ<90°
∴cosθ=
=
,
∴在△ABC中,由余弦定理知BC=
=30
(海里),
∴该船的行驶速度为
=45
(海里/小时).
故答案为:45
.
| ||
| 6 |
∴cosθ=
1-
|
| ||
| 6 |
∴在△ABC中,由余弦定理知BC=
| AB2+AC2-2AB•AC•cosθ |
| 3 |
∴该船的行驶速度为
30
| ||
|
| 3 |
故答案为:45
| 3 |
点评:本题主要考查了余弦定理的应用.考查了学生运用三角函数知识解决实际问题的能力.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知点P(x,y)的坐标满足条件
,O为坐标原点,则直线OP的斜率取值范围是( )
|
| A、[3,5] |
| B、[2,5] |
| C、(-∞,3]∪[5,+∞) |
| D、(-∞,2]∪[5,+∞) |
若a>b,则下列不等式正确的是( )
A、
| ||||
| B、a3>b3 | ||||
| C、ac2<bc2 | ||||
| D、a2>b2 |