题目内容
已知角α的终边在第四象限，且tanα=-
，则sinα+cosα= ．
| 4 |
| 3 |
考点：同角三角函数间的基本关系
专题：三角函数的求值
分析：由同角三角函数基本关系式分别求出sinα，cosα再相加即可．
解答：
解：∴tanα=-
，即
=-
，3sinα=-4cosα．
由于sin2α+cos2α=1，得出cos2α=
，角α的终边在第四象限，所以cosα=
，sinα=-
．
所以sinα+cosα=-
+
=-
．
故答案为：-
．
| 4 |
| 3 |
| sinα |
| cosα |
| 4 |
| 3 |
由于sin2α+cos2α=1，得出cos2α=
| 9 |
| 25 |
| 3 |
| 5 |
| 4 |
| 5 |
所以sinα+cosα=-
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
故答案为：-
| 1 |
| 5 |
点评：本题考查同角三角函数基本关系式的应用：三角式求值．属于基础题．
练习册系列答案
相关题目
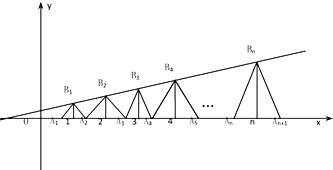已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn） （n∈N*）顺次为一次函数y=