题目内容
已知函数f(x)=2cos(
-
),求该函数的对称轴与对称中心.
| π |
| 3 |
| x |
| 2 |
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:函数的解析式为f(x)=2cos(
-
),令
-
=kπ,k∈z,求得x的解析式,可得函数的图象的对称轴方程.令
-
=kπ+
,k∈z,求得x的解析式,可得函数的图象的对称中心.
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
解:∵函数f(x)=2cos(
-
)=2cos(
-
),
令
-
=kπ,k∈z,求得x=2kπ+
,故函数的图象的对称轴方程为x=2kπ+
,k∈z.
令
-
=kπ+
,k∈z,求得x=2kπ+
,
故函数的图象的对称中心为(2kπ+
,0),k∈z.
| π |
| 3 |
| x |
| 2 |
| x |
| 2 |
| π |
| 3 |
令
| x |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
令
| x |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 3 |
故函数的图象的对称中心为(2kπ+
| 5π |
| 3 |
点评:本题主要考查诱导公式,余弦函数的对称性,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
以(-4,0)、(4,0)为焦点,2a=4的双曲线的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
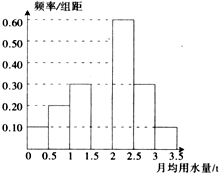 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,