题目内容
某地草莓从2月1日开始上市,通过市场调查,得到草莓的种植成本Q(单位:元/1000kg)与上市时间t(单位:天,从2月1日开始计算)的数据如下表:
(Ⅰ)根据上表数据,从下列函数中(ab≠0)选取一个函数描述草莓的种植成本Q与上市时间t的变化关系,说明选取该函数的理由,并求出相应的解析式.
①Q=at+b;②Q=at2+bt+c;③Q=abt;④Q=a•logbt.
(Ⅱ)利用你选取的函数,求草莓的种植成本最低时的上市时间及最低种植成本.
| 上市时间t | 50 | 100 | 150 |
| 种植成本Q | 3500 | 2000 | 5500 |
①Q=at+b;②Q=at2+bt+c;③Q=abt;④Q=a•logbt.
(Ⅱ)利用你选取的函数,求草莓的种植成本最低时的上市时间及最低种植成本.
考点:函数最值的应用
专题:函数的性质及应用
分析:(1)从给的数据可以看出,函数值随着自变量增大时先减小后增大,所以选择二次函数模型,将给的数据代入可求出a,b,c的值;
(2)即为求该二次函数的最小值,先确定定义域,然后利用配方法求其最小值.
(2)即为求该二次函数的最小值,先确定定义域,然后利用配方法求其最小值.
解答:
解:(1)根据表格中数据函数值随着自变量增大时先减小后增大的特点可知,只有Q=at2+bt+c符合,且此时a>0.
由已知得
,解得a=1,b=-180,c=10000.
所以函数关系为Q=t2-180t+10000,(t∈N).
(2)因为该函数为Q=t2-180t+10000=(t-90)2+1900.
显然当t=90时,Qmin=1900,
故当上市90天时,最低成本为1900元/1000kg.
答:上市90天时,成本最低为1900元/1000kg.
由已知得
|
所以函数关系为Q=t2-180t+10000,(t∈N).
(2)因为该函数为Q=t2-180t+10000=(t-90)2+1900.
显然当t=90时,Qmin=1900,
故当上市90天时,最低成本为1900元/1000kg.
答:上市90天时,成本最低为1900元/1000kg.
点评:本题考查了二次函数在应用题中的应用,以及利用配方法求最值的问题,最后要注意将结果还原为实际问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知函数f(x)=
x2+lnx,?x0∈[1,e],使不等式f(x)≤m,则实数m的取值范围( )
| 1 |
| 2 |
A、m≥1+
| ||
B、m≥
| ||
| C、m≥1 | ||
| D、m≥1+e |
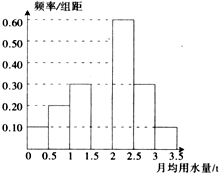 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,