Question

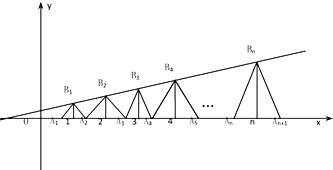已知点列B₁（1，y₁）、B₂（2，y₂）、…、B_n（n，y_n） （n∈N^*）顺次为一次函数y=

1

4

x+

1

12

图象上的点，点列A₁（x₁，0）、A₂（x₂，0）、…、A_n（x_n，0）（n∈N^*）顺次为x轴正半轴上的点，其中x₁=a（0＜a＜1），对任意n∈N^*，点A_n、B_n、A_n+1构成以B_n为顶点的等腰三角形．如果所有的等腰三角形A_nB_nA_n+1中存在等腰直角三角形，则a的取值可以是

 

．

Answer 1

考点：进行简单的合情推理

专题：计算题,推理和证明

分析：当n为奇数、当n为偶数时可分别求得|A_nA_n+1|，作x轴垂线，垂足为C_n，要使等腰三角形A_nB_nA_n+1为直角三角形，必须且只需|A_nA_n+1|=2|B_nC_n|，分n为奇数、偶数两种情况可求得a值．

解答： 解：当n为奇数时，A_n（n+a-1，0），A_n+1（n+1-a，0），所以|A_nA_n+1|=2（1-a）；
当n为偶数时，A_n（n-a，0），A_n+1（n+a，0），所以|A_nA_n+1|=2a；
作x轴垂线，垂足为C_n，则|B_nC_n|=

n

4

+

1

12

，
要使等腰三角形A_nB_nA_n+1为直角三角形，必须且只需|A_nA_n+1|=2|B_nC_n|．
当n为奇数时，有2（1-a）=2（

n

4

+

1

12

），即12a=11-3n．①
当n=1时，a=

2

3

；当n=3时，a=

1

6

；当n≥5，①式无解．
当n为偶数时，有12a=3n+1，同理可求得a=

7

12

．
综上所述，上述等腰三角形A_nB_nA_n+1中存在直角三角形，此时a的值为

2

3

或

1

6

或

7

12

．
故答案为：

2

3

或

1

6

或

7

12

．

点评：本题考查等差数列与函数的综合，考查学生分析问题解决问题的能力，考查分类讨论思想，比较基础．