题目内容
17.已知圆C:(x-$\sqrt{3}$)2+(y-1)2=1和两点A(-t,0),B(t,0),(t>0),若圆上存在点P,使得∠APB=90°,则t的最大值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (x-$\sqrt{3}$)2+(y-1)2=1的圆心C($\sqrt{3}$,1),半径r=1,设P(a,b)在圆C上,则$\overrightarrow{AP}$=(a+t,b),$\overrightarrow{BP}$=(a-t,b),由已知得t2=a2+b2=|OP|2,t的最大值即为|OP|的最大值.
解答 解:圆C:(x-$\sqrt{3}$)2+(y-1)2=1的圆心C($\sqrt{3}$,1),半径r=1,
设P(a,b)在圆C上,则$\overrightarrow{AP}$=(a+t,b),$\overrightarrow{BP}$=(a-t,b),
∵∠APB=90°,∴$\overrightarrow{AP}$⊥$\overrightarrow{BP}$,
∴$\overrightarrow{AP}$•$\overrightarrow{BP}$=(a+t)(a-t)+b2=0,
∴t2=a2+b2=|OP|2,
∴t的最大值即为|OP|的最大值,等于|OC|+r=2+1=3.
故选:C.
点评 本题考查实数的最大值的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
7.若执行如图所示的程序框图,输出S的值为4,则判断框中应填入的条件是( )

| A. | k<18 | B. | k<17 | C. | k<16 | D. | k<15 |
8.司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
(Ⅱ)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | |||
| 女性司机人数 | |||
| 合计 |
参考公式与数据:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
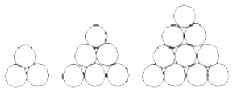 在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示). 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF=$\frac{1}{2}$AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证:
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,EF=$\frac{1}{2}$AB,平面BCF⊥平面ABCD,BF=CF,G为BC的中点,求证: