题目内容
9.f(x)=|x-a|+|2x+1|(1)a=1,解不等式f(x)≤3;
(2)f(x)≤2a+x在[a,+∞)上有解,求a的取值范围.
分析 (1)通过讨论x的范围,求出各个区间上的不等式的解集取并集即可;
(2)求出f(x)的最大值,问题转化为不等式化为2x+1≤3a有解,求出a的范围即可.
解答 解:(1)a=1时,f(x)=|x-1|+|2x+1|,
故$\left\{{\begin{array}{l}{x<-\frac{1}{2}}\\{1-x-1-2x≤3}\end{array}}\right.$,或$\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤1}\\{1-x+2x+1≤3}\end{array}}\right.$或$\left\{{\begin{array}{l}{x>1}\\{x-1+2x+1≤3}\end{array}}\right.$,
解得:$-1≤x<-\frac{1}{2}$或$-\frac{1}{2}≤x≤1$或x∈∅,
所以原不等式解集为{x|-1≤x≤1}.
(2)∵x∈[a,+∞),
∴f(x)=|x-a|+|2x+1|=x-a+|2x+1|≤2a+x,
故|2x+1|≤3a有解,所以a≥0,
∴不等式化为2x+1≤3a有解,
即2a+1≤3a⇒a≥1.
点评 本题考查了解绝对值不等式问题,考查绝对值的性质以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
4. 下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
 下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )
下图为某一函数的求值程序框图,根据框图,如果输出的y的值为3,那么应输入x=( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
14.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
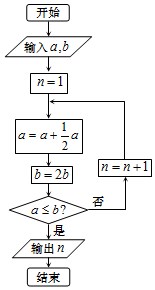 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4.
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5和2,则输出的n=4.