Question

11．如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，EF=$\frac{1}{2}$AB，平面BCF⊥平面ABCD，BF=CF，G为BC的中点，求证：
（1）OG∥平面ABFE；
（2）AC⊥平面BDE．

Answer 1

分析 （1）推导出OG∥AB，由此能证明OG∥平面ABFE．
（2）推导出AC⊥BD，FG⊥平面ABCD，从而EO⊥平面ABCD，进而EO⊥AC，由此能证明AC⊥平面BDE．

解答 证明：（1）∵四边形ABCD是菱形，AC，BD相交于点O，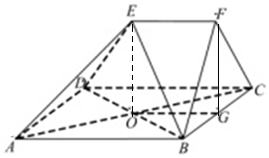
∴O是AC中点，
∵G为BC的中点，∴OG∥AB，
∵OG?平面ABFE，AB?平面ABFE，
∴OG∥平面ABFE．
（2）∵四边形ABCD是菱形，AC，BD相交于点O，
∴AC⊥BD，O是AC中点，
∵G为BC的中点，∵EF∥AB，EF=$\frac{1}{2}$AB，平面BCF⊥平面ABCD，BF=CF，
∴FG⊥平面ABCD，∴EO⊥平面ABCD，∴EO⊥AC，
∵EO∩BD=O，∴AC⊥平面BDE．

点评 本题考查线面垂直、线面平行的证明，考查空间中线线、线面、面面间的位置关系，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想、函数与方程思想是，是中档题．