题目内容
设平面直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为ρ2=
,点F1、F2为其左、右焦点,直线l的参数方程为
(t为参数,t∈R)
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的动点P到直线l的最大距离.
| 12 |
| 3cos2θ+4sin2θ |
|
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的动点P到直线l的最大距离.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)消去参数,可得直线l的普通方程和曲线C的直角坐标方程;
(2)设P(2cosθ,
sinθ),则d=
,即可求曲线C上的动点P到直线l的最大距离.
(2)设P(2cosθ,
| 3 |
|
| ||
|
解答:
解:(1)直线l的参数方程为
(t为参数,t∈R),普通方程为x-y-2=0;
曲线C的极坐标方程为ρ2=
,直角坐标方程为
+
=1;
(2)设P(2cosθ,
sinθ),则d=
,
∴θ-θ0=
,即P(-
,
)时,曲线C上的动点P到直线l的最大距离为
+
.
|
曲线C的极坐标方程为ρ2=
| 12 |
| 3cos2θ+4sin2θ |
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(2cosθ,
| 3 |
|
| ||
|
∴θ-θ0=
| π |
| 2 |
4
| ||
| 7 |
3
| ||
| 7 |
| ||
| 2 |
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列函数是正整数指数函数的是( )
A、y=(1-
| ||
| B、y=2x2(x∈N) | ||
| C、y=(a-3)x(a>3,且x∈N) | ||
D、y=(
|
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=3-x2 | ||
B、y=
| ||
| C、y=log2|x| | ||
| D、y=x3+1 |
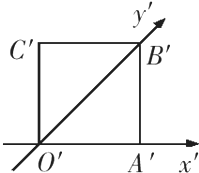 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )
一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )