题目内容
设函数f(x)=|x+2|+|2x-1|
(Ⅰ)求函数y=f(x)的最小值;
(Ⅱ)若f(x)≥mx-
+
恒成立,求实数m的取值范围.
(Ⅰ)求函数y=f(x)的最小值;
(Ⅱ)若f(x)≥mx-
| m |
| 2 |
| 5 |
| 2 |
考点:绝对值不等式的解法,函数恒成立问题
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)由绝对值的含义,讨论当x≤-2时,当-2<x<
时,当x≥
时,去掉绝对值,由一次函数的单调性可得值域,进而得到最小值;
(Ⅱ)令g(x)=mx-
+
,则g(x)的图象恒过定点(
,
),画出y=f(x)和y=g(x)的图象,通过图象观察,即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)令g(x)=mx-
| m |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:
 解:(Ⅰ)当x≤-2时,f(x)=-x-2+1-2x=-3x-1,此时f(x)≥5;
解:(Ⅰ)当x≤-2时,f(x)=-x-2+1-2x=-3x-1,此时f(x)≥5;
当-2<x<
时,f(x)=x+2+1-2x=3-x,此时
<f(x)<5;
当x≥
时,f(x)=x+2+2x-1=3x+1,此时f(x)≥
.
则有f(x)的值域为[
,+∞),
即有x=
时,f(x)取得最小值
;
(Ⅱ)令g(x)=mx-
+
,则g(x)的图象恒过定点(
,
),
画出y=f(x)和y=g(x)的图象,
由图象可得m的取值范围为[-1,3].
 解:(Ⅰ)当x≤-2时,f(x)=-x-2+1-2x=-3x-1,此时f(x)≥5;
解:(Ⅰ)当x≤-2时,f(x)=-x-2+1-2x=-3x-1,此时f(x)≥5;当-2<x<
| 1 |
| 2 |
| 5 |
| 2 |
当x≥
| 1 |
| 2 |
| 5 |
| 2 |
则有f(x)的值域为[
| 5 |
| 2 |
即有x=
| 1 |
| 2 |
| 5 |
| 2 |
(Ⅱ)令g(x)=mx-
| m |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
画出y=f(x)和y=g(x)的图象,
由图象可得m的取值范围为[-1,3].
点评:本题考查绝对值的定义,考查一次函数的单调性的运用:求值域,考查数形结合的思想方法,考查直线恒过定点以及不等式恒成立问题的解法,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=1,AC=2,BC=
,AA1=
,则球O的表面积为:( )
| 5 |
| 11 |
A、
| ||
| B、18π | ||
| C、32π | ||
| D、16π |
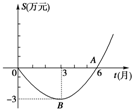 2009年某个体企业受金融危机和国家政策调整的影响,经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来的累积利润S(万元)与时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系,0≤t≤12).请根据图象提供的信息解答下列问题:
2009年某个体企业受金融危机和国家政策调整的影响,经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来的累积利润S(万元)与时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系,0≤t≤12).请根据图象提供的信息解答下列问题:
 如图,直角△ABC,∠A=90°,BC=2AB,AH⊥BC,BH=1,点M在AH上,且AH=3AM,则
如图,直角△ABC,∠A=90°,BC=2AB,AH⊥BC,BH=1,点M在AH上,且AH=3AM,则